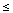 x
< L/2, but 0 for L/2
x
< L/2, but 0 for L/2
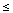 x
x
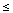 L
L
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 8 May 2000
If you wish to print a nicely formatted version of this chapter, you may download the rtf file, which will be interpreted and opened by Microsoft Word or the pdf file, which will be interpreted and opened by Adobe Acrobat Reader.
(Some remarks for the instructor).
In this section we calculate several Fourier series. As we know, to find a Fourier series simply means calculating various integrals, which can often be done with software or with integral tables. Since performing integrals is not much more interesting in the modern age than long division, our goals in this section will be to get a visual and analytic impression of what to expect from Fourier series, and to understand the rôle of symmetry in the calculations. Many of the calculations in this chapter are available in a Mathematica notebook or Maple worksheet.
f(x) = 1 for 0
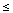 x
< L/2, but 0 for L/2
x
< L/2, but 0 for L/2
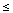 x
x
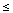 L
L
and
g(x) = x, 0
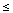 x < L.
x < L.
The functions have not been defined at the points of discontinuity, but as we know, the Fourier series will converge there to the average of the limit from the left and the limit from the right. The end point L is essentially a jump point, because the periodic extension of the functions make the values x=L and x=0 equivalent.
Here is a graph of the function f, called a "square pulse" or "square wave"
(when extended periodically):
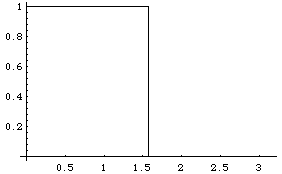
The length L has been chosen as
 .
.
We want to represent these functions in the form
Model Problem IV.1. Use software to calculate the full Fourier series for the function f(x) as defined above, and investigate its convergence.
Solution. The formulae for these coefficients were given in Chapter II:
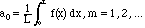
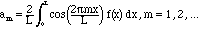
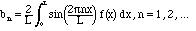
 )
)
The sort of expression we got for the bn simplifies in a way which arises often in Fourier series for elementary functions: If n=2k is even, b2k = 0. Thus only odd terms survive, in which case
 (2k+1)).
(2k+1)).
With one sine term:
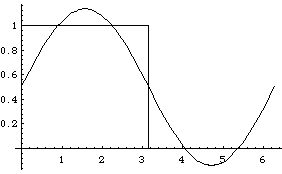
With three sine terms:
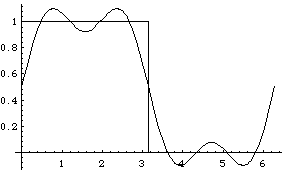
With seven sine terms:
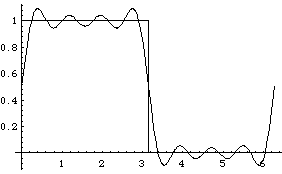
And so on. We call attention to the systematic overshoot that occurs at the edges of the jump. Curiously, the size of this last overshoot does not tend to 0 as we include more terms. (You can see this in an animation prepared for us by Georgia Tech student Ning Wu; the fact that Ning's function has vertical range -1 to 1 is not significant for this purpose.) The bumps next to the jump get thinner rather than shorter. This is known as the Gibbs phenomenon.
Model Problem IV.2. We can now investigate some questions about the excitation of mechanical resonances. Suppose that experiments by K. Battle at the Wiener Staatsoper in Austria show that a crystal goblet will shatter if the intensity of the tone at frequency 1760 Hz (high A) exceeds .01. We use physical units in which the proportionality between the power and the square of the amplitude is 1, i.e., we define the intensity simply as
Question: What amplitude A will cause the glass to shatter in our laboratory?
Solution. The issue is essentially to estimate the magnitude of the Fourier coefficient for our function corresponding to the frequency 1760 Hertz.
The mapping from functions to their Fourier coefficients is linear. Hence the coefficients can be obtained from the ones we just calculated.
Step 1. Scale the independent variable by replacing x with t and L with 1/352.
Step 2. Multiply all the coefficients by A.
The harmonic with frequency 1760 is the one with n=5, so the Fourier coefficients corresponding to this frequency are
 )
)
 2). The amplitude A above which the glass will
shatter is
2). The amplitude A above which the glass will
shatter is  /4,
numerically about 0.78539816.
/4,
numerically about 0.78539816.
 x
x  1,
sometimes designated x mod 1. Watch it converge.
1,
sometimes designated x mod 1. Watch it converge.
Solution. (For more details on the calculations, see the Mathematica notebook or the Maple worksheet. For x between 1 and 2, the function is (x-r1L), for x between 2 and 3 it is (x-2), etc. Its graph has a sawtooth shape:
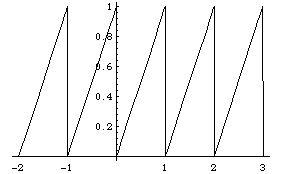
Because the interval has length 1, the
Fourier basis functions are
1, cos(2n x), and
sin(2n
x), and
sin(2n x).
x).
The Fourier coefficients are calculated as:
 )
)
Let us get an impression of how the series converges, by
plotting the contributions of the first two sines, and then of six sines:
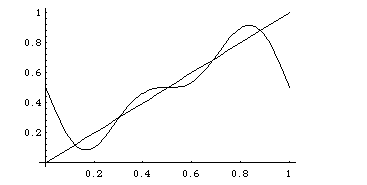
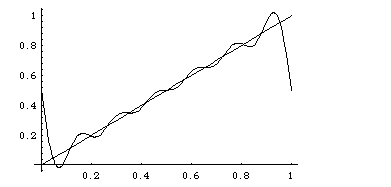
We also recall that on a longer interval, the
Fourier series produces a periodic function:
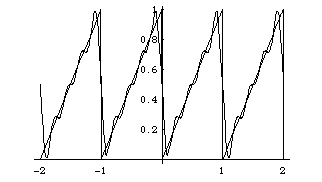
The Fourier series is converging nicely to the function except at the end-points of the interval, which are places where the full periodic saw-tooth function has jumps, and we saw something similar with the square pulse. In both cases we see numerical evidence for the theorem that the Fourier series converges to f(x) where f(x) is continuous, and where it has a jump, the Fourier series converges to the average of the upper and the lower value at the jump.
Let's try out a different sort of example, where we need to integrate numerically (see notebook).
Model Problem IV.4. Find the Fourier series for the function
sin( /x).
/x).
Solution. The integrals called for are not in the integral tables. Indeed,
most integrals are not in the integral tables, even when they are
nowhere near as wild as this function (ask yourself what happens near x=0). In
the information age this is no barrier. We simply call on the software to do
the integrals numerically. Since the function
sin( /x)
is odd in x, the coefficients associated with even functions,
am,
will all be zero. With some complaints
about the convergence, the software calculates the first six sine coefficients as:
/x)
is odd in x, the coefficients associated with even functions,
am,
will all be zero. With some complaints
about the convergence, the software calculates the first six sine coefficients as:
-0.3071329778789654123
0.5062509679699521912
-0.271449220623610834
-0.2561291634161970945
0.1947511859947028479
0.2192911372159977088
Let us plot the Fourier series with these six
terms and compare with the function itself:
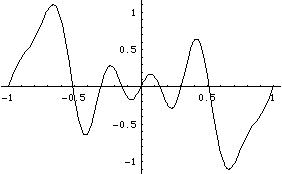
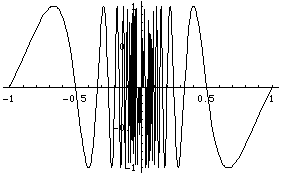
Notice that the convergence is pretty good away from the nasty singularity at x=0. In effect, truncating the Fourier series has filtered out the high-frequency oscillations.
Model Problem IV.5. Find the Fourier series for a function which is square-integrable but has an infinite jump.
Solution. The example we look at is x-1/3.
Like the previous example, the function is odd,
and there will only be sine contributions.
The first several coefficients are numerically:
1.710689953277251171
0.3736036030974259086
0.7368949814369842807
0.2752161613201822172
0.5010701734296802681
0.2252029789384463762
Here is a comparison of the function and its Fourier approximation:
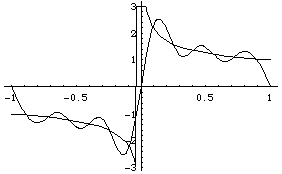
Think about the series calculation at x=0 and at x=+/-1. Did what you expected happen?
As we have seen in computations, symmetries can be used to simplify the computation of Fourier series. Recall that a function is even if f(-x)=f(x) for all x, and odd if f(-x) = -f(x) for all x. If f is a periodic even function, then all of the sine coefficients bn = 0: bn is the inner product of f with a sine function, but any even function and any odd function are orthogonal on the interval [-A, A]. (If f(x) is periodic with period L, then we can analyze it on any interval of length L, so even if it is originally defined on [0,L], we can just as well look at it on [-L/2, L/2]. Look at a graph of a periodic function to understand why.) For similar reasons, if f is periodic and odd, all the coefficients am = 0.
Any function can be written as the sum of an even function and an odd function,
and the Fourier series picks out the two parts. If, for instance, we want to
find the Fourier series of a function such as
 x - x2, -
x - x2, -

 x
x 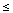
 ,
we can save some work by thinking about the symmetries.
,
we can save some work by thinking about the symmetries.
Model Problem IV.6. Use symmetries to efficiently find the Fourier
series for the function
 x - x2 on
the interval -
x - x2 on
the interval - < x <
< x <
 .
.
Solution.
This function is neither even nor odd when we change x into -x, but its
"odd part" is
 x, and its "even part" is
-x2. The sine coefficients in the
Fourier series will come entirely from the odd part and the even coefficients
entirely from the even part; -x2
is orthogonal to all the Fourier cosine
functions, and
x, and its "even part" is
-x2. The sine coefficients in the
Fourier series will come entirely from the odd part and the even coefficients
entirely from the even part; -x2
is orthogonal to all the Fourier cosine
functions, and
 x is orthogonal to all the
Fourier sine functions.
Moreover, the symmetry can be used to change the integration range so that
it begins at 0:
x is orthogonal to all the
Fourier sine functions.
Moreover, the symmetry can be used to change the integration range so that
it begins at 0:
The coefficients bn are calculated as follows:
The product of two odd functions is even, so this integral is:
The final result was calculated by software. In a calculus class you would
have probably calculated it by integration by parts.
The calculation of the coefficients an can also be simplified. First, notice
that only -x2 contributes:
The value of this integral is
When you combine these, you have the Fourier coefficients for
 x - x2
on this interval.
x - x2
on this interval.
 ) = (-1)n.
) = (-1)n. /2) = (-1)k i,
/2) = (-1)k i,
 ),
where
),
where
 ,
the argument of z, is the polar angle in the
complex plans, and r = |z| (the modulus of z) is the distance from the origin.
One of the truly great things about this formula is that is allows us to
replace calculations with trigonometric functions with much easier calculations
with exponential functions. As an example, let us think of how to calculate
the Fourier series for the function f(x) = x, 0
,
the argument of z, is the polar angle in the
complex plans, and r = |z| (the modulus of z) is the distance from the origin.
One of the truly great things about this formula is that is allows us to
replace calculations with trigonometric functions with much easier calculations
with exponential functions. As an example, let us think of how to calculate
the Fourier series for the function f(x) = x, 0
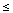 x < L (repeated
periodically, if you wish, outside this interval - notice that this is not a
centered interval, so this calculation is different from the one done above.).
a0 is the average of the function, so, obviously, a0 = L/2. For the other am,
we have to calculate integrals of the form
x < L (repeated
periodically, if you wish, outside this interval - notice that this is not a
centered interval, so this calculation is different from the one done above.).
a0 is the average of the function, so, obviously, a0 = L/2. For the other am,
we have to calculate integrals of the form
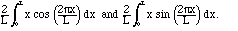
If you don't have software or integral tables handy, you can do these integrals with integration by parts. Or you can reason as follows:
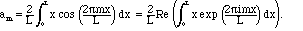
Model Problem IV.7. Evaluate this integral by a method different from integration by parts.
Solution. We can use the following useful trick:
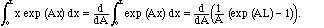 (4.2)
(4.2)
After the calculation, we set A=2
 i m/L. Calling the integral in (4.2)
INT, we find
i m/L. Calling the integral in (4.2)
INT, we find
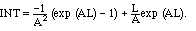
which starts looking nice after we substitute A=2
 im/L, which reveals that
these exponential terms are both equal to 1:
im/L, which reveals that
these exponential terms are both equal to 1:
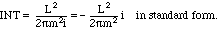 (4.3)
(4.3)
This is purely imaginary, so all am = 0.
Solution. STOP! Don't go back to the beginning of the calculation. We don't have to start all over, since
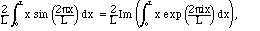
which is the integral we already did. From (4.3) we see that this imaginary part is just
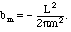
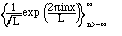
These are simply related to the sines and cosines by Euler's formula (4.1) and its easy consequence:
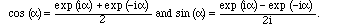
Definition IV.9. The Fourier exponential series is an expansion (for an arbitrary square-integrable function):
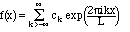 (4.4)
(4.4)
Since the exponential functions are an orthonormal set, a familiar kind of
calculation shows us that the formula for ck
Notice the tricky minus sign - this is a place where the complex conjugate in
the inner product is important.
Let's observe how much more convenient this formula is than the one without
complex numbers. There is only one sum, not two sums and a constant term.
There is only one formula for ck, not separate ones for a0, am, and bn. The
constant term c0 fits in with all the others, for instance, and is not put
aside as a special case. The Parseval formula (3.4) is now much simpler:
Here, the coefficients for g have the tildes. In particular,
Notice that the Parseval formula is similar to the
Pythagorean theorem, since, other
than the normalization factor L, it states that a certain length squared is
equal to the sum of the squares of its components in an orthogonal basis. We
see here, however, that the space in which f lives is infinite-dimensional.
The important thing to know is that the
Fourier exponential series is
completely equivalent to the usual "full" Fourier series. We will later look
at the Fourier sine and Fourier cosine series, which are truly different
series, but the exponential series is not. If we substitute with
Euler's formula,
the full series becomes the exponential series
or vice versa.
We can recombine ck with c-k as follows:
From this we get the connecting formulae that:
a0 = c0, am = cm+c-m, and bn = i (cn - c-n}).
(4.8)
Another useful fact to know about Fourier series is that you can normally
safely differentiate them and integrate them, as long as the functions you are
representing are periodic and differentiable. Actually, even if the function
is not smooth, these manipulations are still often possible. This topic is
explored in the next chapter.
Link to
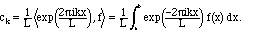 (4.5)
(4.5)
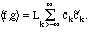 (4.6)
(4.6)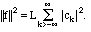 (4.7)
(4.7)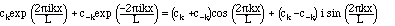
Exercises.
 ,
,
 ], and b) the interval [0,1].
], and b) the interval [0,1].