Blitz of Recent Research
NOTE: This page is for a fast glimpse. Content is incomplete, inaccurate, and non-rigorous. Please kindly refer to publications for important literature.
Asymptotics in (stochastic) dynamics and differential equations.
1. Structure preserving integration
1a. Explicit symplectic integrators for nonseparable Hamiltonians
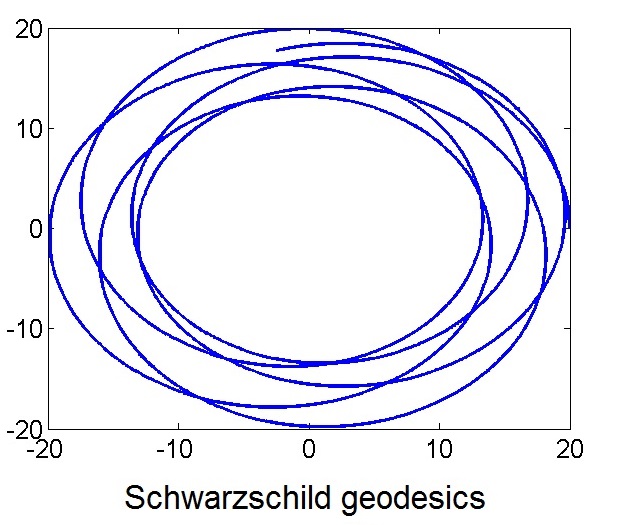 |
Symplectic integrators have favorable long time accuracies. By 1990 how to construct explicit and high-order symplectic integrators had been solved for separable Hamiltonians (i.e., [Tao 16 PRE] provides a solution based on augmented phase space and multiscale methods (including KAM theory). For integrable systems, trajectory error is shown to be linearly growing with long simulation time, which is advantageous to exponential or quadratic growth of nonsymplectic methods. For nonintegrable systems, statistical accuracy was also numerically observed. |
1b. A special case: charged particles
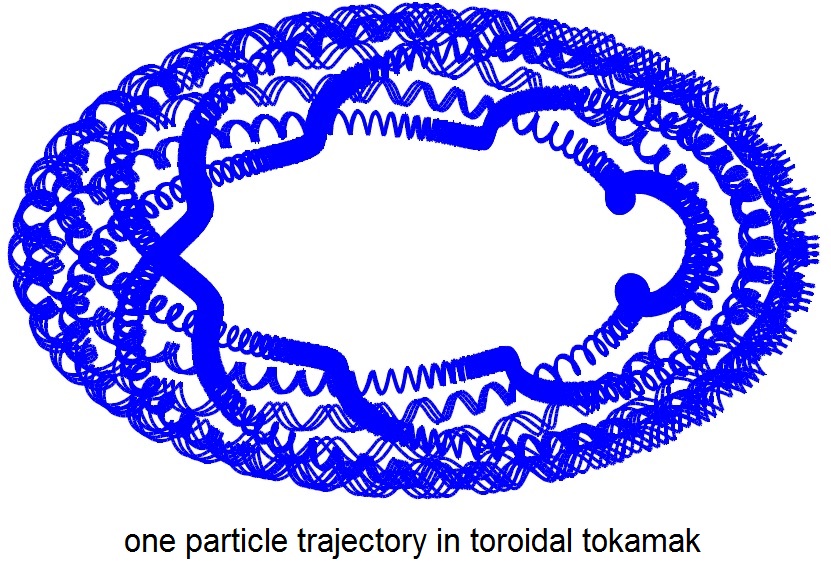 |
The above method (1a) is symplectic only in an augmented phase space. Although pleasant long time accuracy was obtained (the main reason to use a symplectic integrator), it would still be nice to hope for symplecticity in the original phase space. [Tao 16 JCP] describes how to do so for Hamiltonians in the form of
|
1c. Discontinuous Hamiltonians
 |
Coming soon… |
1d. Multiscale problems
How to preserve symplecticity or nearly preserve the invariant distribution in multiscale setups? See below (e.g., 2a).
2. Efficient numerical methods based on multiscale analysis
2a. FLow AVeraging integratORS for stiff (stochastic) mechanical systems
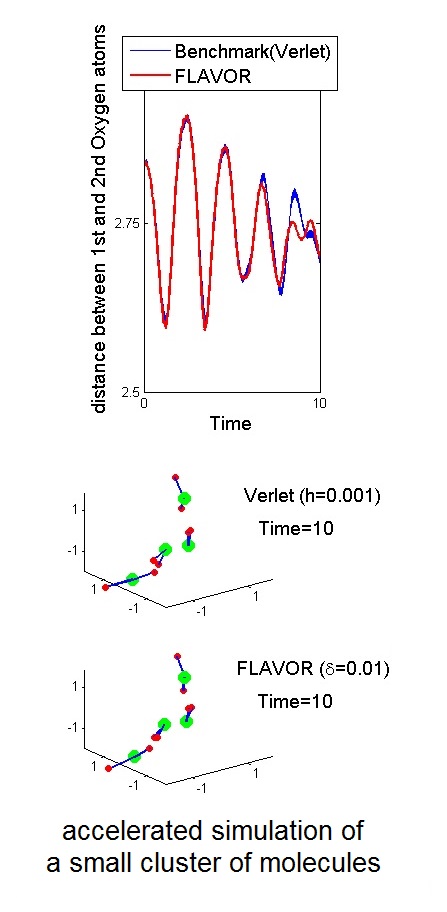 |
Largely based on asymptotic methods of averaging and homogenization, breakthroughs have been made to efficiently simulate multiscale systems such as 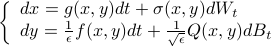
The goal is to use a timestep that does not resolve the y (fast) dynamics. This way, the computational cost remains bounded as Sometimes, such an upscaled simulation can even be done for systems without identified slow or fast variables, i.e., 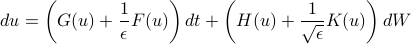
But what happens if the (noiseless) system is mechanical, which has conservation laws, or a stochastic generalization that has an invariant distribution? Most available approaches do not preserve these structures, because they are destroyed after the x (slow) vector field gets averaged. [Tao, Owhadi & Marsden 10 MMS] proposed a solution to this open problem by averaging flows instead of vector fields. It turns a single-scale integrator into a multiscale one, and inherits its structure preservation properties. Accuracy was also quantified as 2-scale convergence (pointwise in x but weak in y) was established. However, x & y need not to be identified, and the method needs only the u equation (under commonly assumed conditions). An application to the simulation of circuits is contained in [Ober-Bloebaum & Tao et al. 13 JCP]. |
2b. Simply improved averaging for weakly nonlinear systems
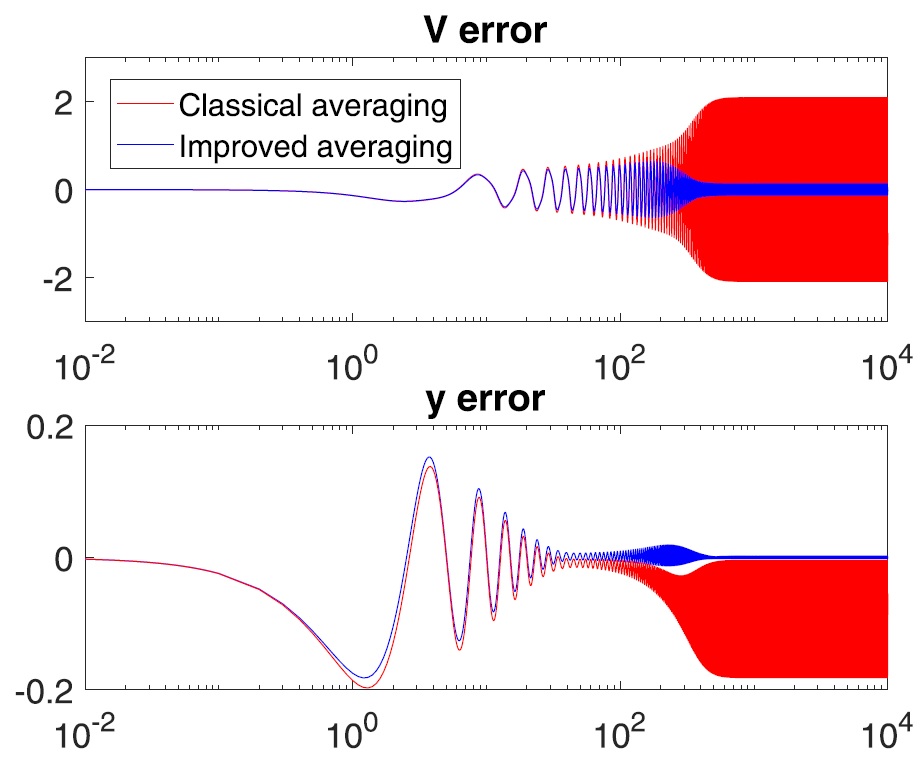 |
Most averaging-inspired numerical methods are based on 1st-order averaging, which alone has an error of [Tao 18 CNSNS] suggests a new, analytical 1st-order averaging approach for |
2c. exoplanet, old & new
 |
[Li, Holman, & Tao 16 ApJ] and more coming soon… |
2d. trapped in and passage through resonance
Coming soon…
3. Multiscale control
Our abilities to interact with practical systems are constrained by physical and technological limitations. Thus, we proposed multiscale control as a way to overcome a lack of controllability. The key idea is, the restricted control may indeed be inadequate to immediately change the system; however, if it can be introduced at a microscopic temporal or spatial scale, its contributions can accumulate and alter the macroscopic behavior in a desired fashion.
3a. Resonance-enabled trajectory-tracking of an otherwise-linear oscillator
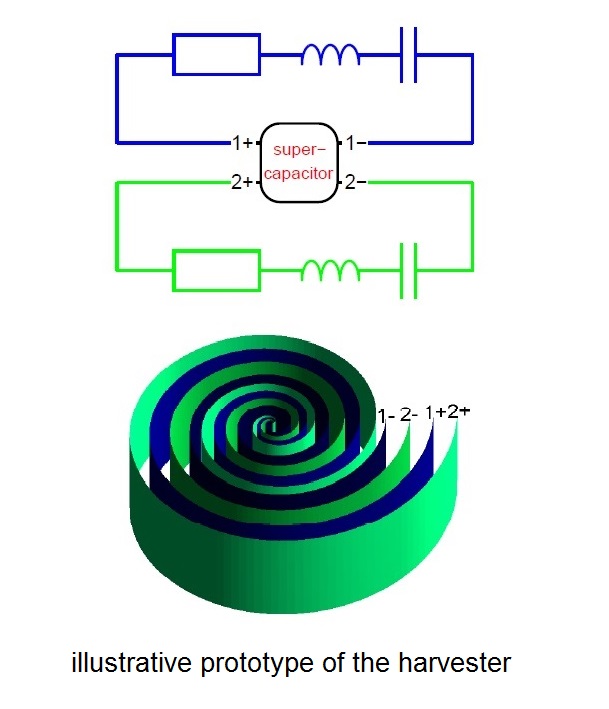 |
[Tao & Owhadi 16 ARMA] provides a theoretical demostration of multiscale control. It shows how to let the oscillation amplitude of an otherwise harmonic oscillator track an arbitrary function, based on physically implementable parametric perturbations. It also proposes a generalization of parametric-resonance, which can possibly serve as a mechanism for harvesting energy in the face of strong dissipations. This paper also provided refined error bounds of asymptotic analysis. |
3b. Simultaneous trajectory-tracking of multiple weakly nonlinear oscillators
 |
Based on the above resonant control idea (3a), [Xie & Tao 19 ACC] shows how to independently control many oscillators by a shared parametric perturbation, even when the oscillators are subject to small noise, dissipation, and nonlinearity. A simulated demonstration is on YouTube, in which an array of tunable light bulbs animates a video as the circuit of each bulb is separately controlled by a shared external electromagnetic field. |
3c. Capacitive Parametric Ultrasonic Transducers (CPUT) for wireless energy transfer
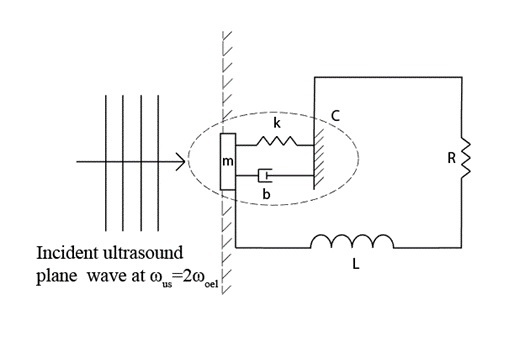 |
[Surappa, Tao, & Degertekin 18 UFFC] shows it is possible to wirelessly transfer energy via parametric resonance. An engineering device is designed to transform the mechanical energy of external ultrasound at specific frequency into eletric energy in a circuit. The theoretical analysis and parameter design used the above improved averaging (2b). |
3d. Nonlinear destabilization of a simplified DNA model
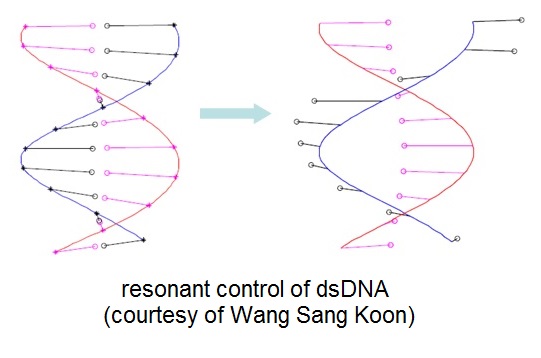 |
In [Koon, Owhadi, Tao, & Yanao 13 Chaos] and ongoing research, we applied the multiscale control idea to selectively control coarse-grained models of DNAs. The ultimate goal is a precision therapy. |
3e. Space-time phononic crystals with anomalous topological edge states
What can happen if you shake a medium in which acoustic wave propagates? [Oudich, Deng, Tao, & Jing 19 submitted] and more coming soon…
4. Numerical methods for quantifying rare events in stochastic dynamical systems
4a. Methods for hyperbolic periodic orbit
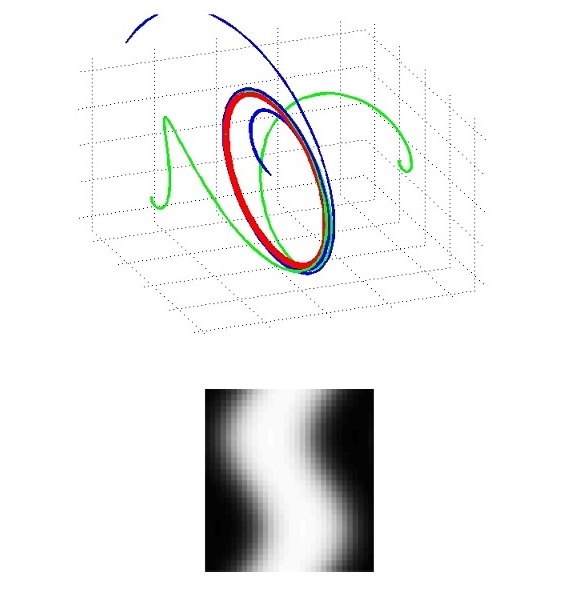 |
Small noise induced metastable transition in a gradient system (reversible Markov process) crosses separatrix at a saddle point. [Tao 18 Physica D] discusses an alternative possibility, where such a transition in nongradient systems (irreversible) crosses a hyperbolic periodic orbits and has infinite arc length. Numerical methods for identifying hyperbolic periodic orbits and for approximating the transition are proposed based on adaptations of String method and gMAM. Dynamical structures of sheared Allen–Cahn on 2-torus are also explored. For example, a YouTube video shows a hyperbolic period orbit. |
4b. The inertial Langevin equation
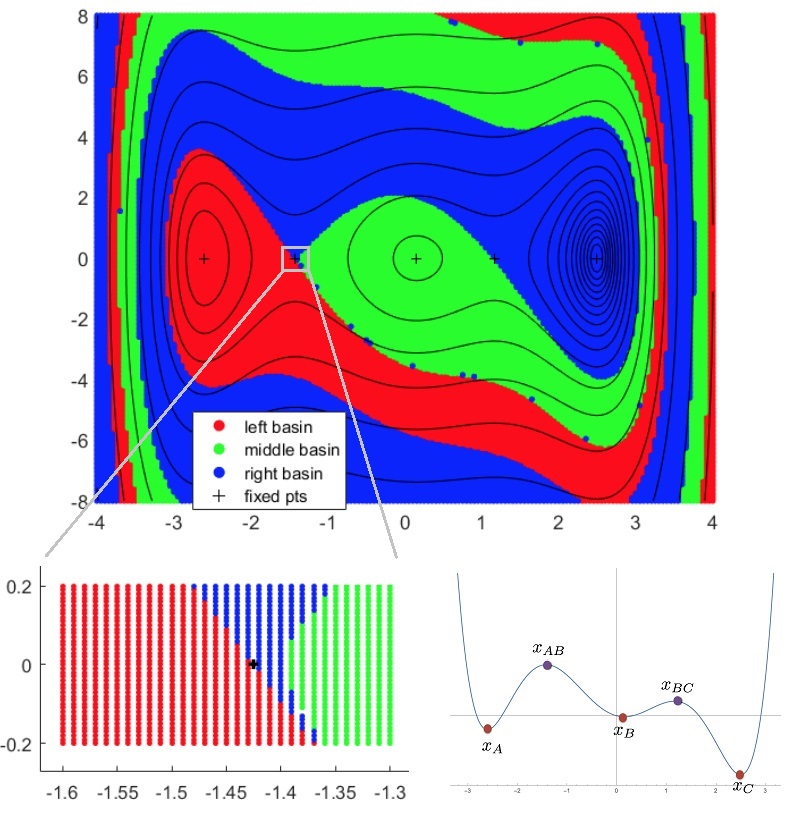 |
[Souza & Tao 18 EJAM] considers rare events in small noise inertial Langevin: 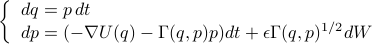
Its overdamped limit is reversible and well understood. Other cases, however, can exhibit fundamentally different behaviors. For example, underdamped transition between ‘‘adjacent’’ potential wells may not be a concatenations of heteroclinics, due to inertial effects, and its rate is not simply given by a barrier height. Numerical methods are constructed accordingly. |
5. Machine learning applications
5a. Learning algorithms based on (stochastic) dynamics
Optimization
Sampling
Coming soon…
5b. Learning multiscale dynamics from data
[Dylewsky, Tao, & Kutz 19 PRE] and more coming soon…
Research has been generously supported by NSF.
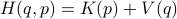 ).
However, how to do so for general, nonseparable Hamiltonians, which also model important systems, was an open problem.
).
However, how to do so for general, nonseparable Hamiltonians, which also model important systems, was an open problem.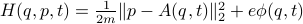 , based on a different approach (generating function-based augmentation of Runge-Kutta method).
Such Hamiltonians correspond (but are not limited) to non-relativistic charged particles in time-dependent eletromagnetic fields. This time-dependent case was also an open problem, of interest to plasma and particle physics.
, based on a different approach (generating function-based augmentation of Runge-Kutta method).
Such Hamiltonians correspond (but are not limited) to non-relativistic charged particles in time-dependent eletromagnetic fields. This time-dependent case was also an open problem, of interest to plasma and particle physics.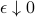 .
.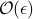 . When
. When  is not infinitesimal, reducing the constant factor in the error bound is particularly beneficial, especially because higher-order averaging of many problems is practically unmanagable due to multiple frequencies.
is not infinitesimal, reducing the constant factor in the error bound is particularly beneficial, especially because higher-order averaging of many problems is practically unmanagable due to multiple frequencies.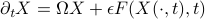 with anti-Hermitian
with anti-Hermitian 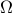 , which for instance models weakly nonlinear waves and coupled oscillators. Numerical methods based on this approach and an existing technique of filtered-average are also constructed and demonstrating significantly improved accuracy.
, which for instance models weakly nonlinear waves and coupled oscillators. Numerical methods based on this approach and an existing technique of filtered-average are also constructed and demonstrating significantly improved accuracy.