Introduction
Conventional wheel suspension system relies on the upward freedom
of wheels relative to the load carried by wheels to overcome
obstacles and reduce shock on the load. It uses strong weight bearing
spring or equivalence to support the load on wheels.
In one extreme application, the in-line roller skate, applying the
conventional suspension system will inevitably increase the gravity
center of the skater because of the upward freedom of the wheels.
Can we have a wheel suspension mechanism which can keep the gravity
center of the load as low as if no suspension system were used,
which uses none or little spring (or equivalence) and thus introduces
no vibrations commonly associated with them, and which is efficient
even for relatively large obstacles ? Here we study a non conventional wheel
suspension mechanism which seems to give positive answers to
the above questions.
Since the invention of the wheel, the fundamental
mechanism of wheel suspension system has not changed.
Whether it is in the form of
spring sheet, trailing arm, leading arm or telescope suspension,
they all are based on the same idea that when the wheel
encounters an obstacle, we want
the wheel instead of the load which the wheel
is carrying to bounce up. Therefore
allowing upward freedom of the wheel seems to be inevitable for a wheel
suspension system. Here we introduce a suspension mechanism
which seems to be
just the opposite of the conventional mechanism.
It could function in some situations
where the conventional suspension mechanism fails and could
even outperform the
conventional suspension system in low speed. The new suspension mechanism
complements the existing suspension mechanism and could have
broad applications. We will try to explain the conceptual
ideas here without going into the details of the physical and
mathematical modeling of more complicated variations.
The concept of tangential suspension mechanism
can be easily described
by use of a bicycle front wheel. First we look at a bicycle front wheel with no
suspension system hitting a bump on the road as in Fig. 1.
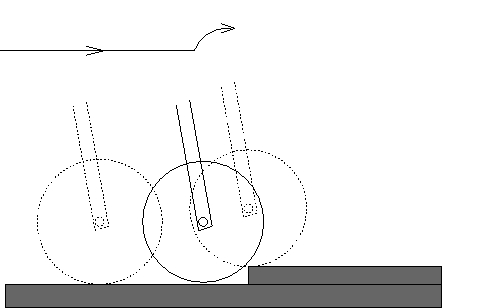
The curve above the bicycle illustrates the trajectory of the gravity
center of the frame.
A sharp corner in the curve indicates that there is a Dirac delta function
in the second derivative of the curve, which corresponds to the
shock the rider feels.
Now let's use a pair of swing arms hanging vertically with one ends
attached to the wheel axle, with the other ends connected pivotally to the
bicycle front forks at a position right below the wheel center.
Assume that the mass of the wheel is negligible comparing to the
mass the whole bicycle. When the wheel encounters an obstacle, unlike
conventional suspension system in which the wheel will bounce up,
the wheel will first stop because the swing arm
is perpendicular to the ground and has essentially no forward component
of force acting on the wheel. Then the swing
arm starts to swing around the wheel center forward and upward.
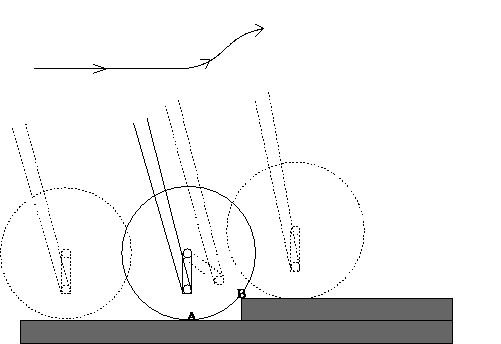
When the swing arm swings pass a critical angle (i.e., the angle
between the line segment
connecting the wheel center and the ground contact point "A" and the
line segment connecting the wheel center and the obstacle contact point "B"),
the net force acting on the wheel will break the equilibrium of the wheel and
drive the wheel to roll over the obstacle.
The resulting trajectory of the mass center of the frame (see the curve
in Fig. 2) will be a continuously
differentiable curve (made of tangentially connected smooth segments)
during this time period, so that there is no
shock force acting on the frame.
Note that in the simple suspension setting of Fig. 2 there is no need
to use any form of weight bearing spring! Besides that, the wheel with tangential
suspension is able to overcome large obstacles at low speed without generating shock
yet still keep the gravity center of the frame as low as if no suspension were used.
Its simplicity could find it applications in almost all the low speed transportation
equipments in the industry and everyday life,
such as wheel chair, roller skate, scooter,
wheel dolly, baby stroller, wheel carts, bicycle, trailer etc.
Compensation of the Rolling Resistance
Under construction.


