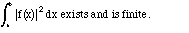
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 7 May 2000
If you wish to print a nicely formatted version of this chapter, you may download the rtf file, which will be interpreted and opened by Microsoft Word or the pdf file, which will be interpreted and opened by Adobe Acrobat Reader.
Many of the calculations in this chapter are available in the form of a Mathematica notebook or Maple worksheet.
(Some remarks for the instructor).
As mentioned in the previous section, perhaps the most important set of
orthonormal functions is
the set of sines and cosines
(2.8).
These are what is known as a
Definition III.1. Square-integrable functions on [a,b] are functions f(x) for which
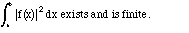
The set of square-integrable functions is usually denoted L2, and we shall see that it is an inner-product space. Later, we will also speak of square-integrable functions on regions in two or three dimensions, in which case we have multiple integrals over those regions.
Roughly speaking, a function on a finite interval is square integrable unless it is infinite somewhere. It can be very discontinuous, and in fact can even be slightly infinite - like the function ln(x), or even |x|-1/3. Most familiar functions are square-integrable.
Definition III.2. An orthonormal set {en(x)} is complete (on
some fixed set of values of x) if for any square integrable function f(x) and
any
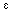 >0, there is a finite
linear combination
>0, there is a finite
linear combination
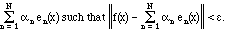
In other words, any reasonable function can be approximated as well as you wish (in the mean-square sense) by finite sums of the set. Indeed, we will say that it is the limit of an infinite series:
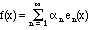
The sense in which this infinite sum converges is, of course, in mean square. (Follow this link for some examples and remarks about convergence of a sequence of functions.) An equivalent way to describe completeness is: An orthonormal set {en(x)} is complete if the statement that
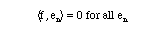
implies f(x) = 0 a.e. This is often a practical way to show that a set is incomplete, because you just have to exhibit a nonzero function which is orthogonal to the entire set.
Unfortunately, it is not as easy to prove completeness as it is to disprove it.
It is a theorem that each of the sets of trigonometric functions
(2.6)-(2.9) is complete and
orthonormal, but the techniques for proving such a theorem are beyond
the scope of this course. To understand the issue better, consider
a finite linear combination of an orthonormal basis,
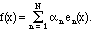
What is the norm of f? Because orthogonality makes the cross terms
vanish, a little calculation shows us that
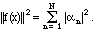
This is an extension of the Pythagorean theorem, since it says that the square of the hypotenuse is the sum of the squares of the lengths of the sides, if the sides are at right angles; only in function space, lots of things can all be at right angles. Suppose we had left out some of the components. Then we would have
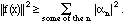
This inequality is still true if N = infinity, and is known as Bessel's inequality. The problem of completeness is that it is not easy to tell if we have included all the basis elements necessary to make both sides equal. We can leave many of them out and still have an infinite number left; in the set of Fourier functions (2.8), for example, we could leave out all the sine functions and still have all the cosine functions left.
The set (2.8) is particularly useful for periodic functions, that
is, functions such that f(x+L) = f(x) for some fixed length L, called the
period, and all x. Since each of the functions in the set is periodic
with period L, any
linear combination
of them is also periodic with the same
period. The completeness just alluded to means that every periodic function
can be resolved into the trigonometric functions of the same period. If the
independent variable is time (which you might prefer to denote t rather than
x), a periodic function of the form sin(2n
 t/L) or cos(2n
t/L) or cos(2n  t/L)
may be detected by your ear and
perceived as a pure musical tone with frequency n/L. Any periodic sound
wave can be resolved into pure musical tones. If you are given a sound
wave f(t), which is periodic with period L you can extract its components of
frequency k/L with formulae (2.12)-(2.14), setting m or n = k. There are two
such components, one with the sine function and the other with the cosine.
This degree of freedom corresponds to the phase of the sound wave, because of
the trig identity:
t/L)
may be detected by your ear and
perceived as a pure musical tone with frequency n/L. Any periodic sound
wave can be resolved into pure musical tones. If you are given a sound
wave f(t), which is periodic with period L you can extract its components of
frequency k/L with formulae (2.12)-(2.14), setting m or n = k. There are two
such components, one with the sine function and the other with the cosine.
This degree of freedom corresponds to the phase of the sound wave, because of
the trig identity:
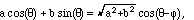 (3.1)
(3.1)
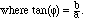
The intensity (power) carried by the component of a sound wave at pure
frequency k/L is proportional to
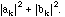
In the next chapter this resolution into pure frequencies is carried out for the square wave and the results are plotted, among other things. You may wish to glance at those plots now to get an intuitive feel for how a Fourier series can approximate a function.
The powerful theorem behind the Fourier series III.3. I will now carefully formulate a theorem which justifies the use of Fourier series for square-integrable functions and tells us several useful facts. Historically, parts of this theorem were contributed by Fourier, Parseval, Plancherel, Riesz, Fischer, and Carleson, and in most sources it is presented as several theorems. For proofs and further details, refer to Rudin's Real Analysis or Rogosinski's Fourier Series.
If f(x) is square-integrable on an interval [a,b], then
a) All of the coefficients am and bn are definite numbers uniquely given by (2.12)-(2.14).
b) All of the coefficients am and bn depend linearly on f(x).
c) The series
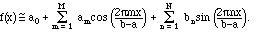
converges to f(x) in the mean-square sense. In other words,
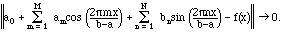
We shall express this by writing
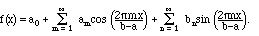 (3.2)
(3.2)
(Remember, however, that this series converges in a mean sense, and not necessarily at any given point.) It is also true that it converges a.e.
d)
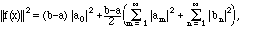 (3.3)
(3.3)
and the right side is guaranteed to converge.
e) If g is a second square-integrable function, with Fourier coefficients
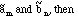
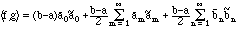 (3.4)
(3.4)
This is known as the Parseval formula.
Conversely, given two square-summable sequences am and an, i.e., real or complex numbers such that
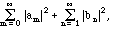
is finite, they determine a square integrable function f(x) uniquely a.e. such that (2.12)-(2.14) and statements b)-d) hold.
There are very similar theorems for the Fourier sine series and the Fourier cosine series series, which are based, respectively, on the orthogonal sets (2.5) and (2.7). Let's stand back and think about what this big theorem tells us. Square-integrable functions are very general, so this is telling us that any reasonable function can be approximated arbitrarily well, in the r.m.s. sense, by a "trigonometric series." We have a formula to generate the coefficients, and in fact a full correspondence between the square-integrable functions and the square-summable sequences. The square-integrable functions L2 form an inner product vector space. The set of double sequences {am,bn} is also a vector space with an inner product given by (3.4). You can think of each object in this space as a vector with an infinite number of components, some of which are denoted am and others bn.
Here are some examples showing why mean-square approximation is not always good enough. At a later stage we shall discuss when Fourier series converge at individual points. We shall see that if f(x) is continuous near x, the Fourier series converges at x.
If you look at the various Fourier series that are plotted in the next chapter, you will see that the crazy phenomenon of Example 2 doesn't happen. In fact, the convergence is very good except at the ends of the intervals or at places where the function is discontinuous. If you look at the periodic extension of a function, you see that the end of an interval is a place where there is likely to be a discontinuity, and it is when this happens that the series did not converge at the end of the interval. (A good example is f(x) = x on the basic interval [0,L].) What we observe is described by a general theorem, which we now formulate.
A function is said to be piecewise continuous (some say sectionally continuous ) if it is continuous except at a discrete set of jump points, where it at least has an identifiable value on the left and a different one on the right. Here is a formal way to state this:
Definition III.5. A function f(x) is piecewise continuous on a finite interval a<=x<=b if it is continuous except at a finite number of points a = x0 < x1 <... < xn = b, and all the one-sided limits
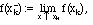
and
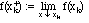
exist (except that we only assume the limit from above at a and the limit from below at b).
Here the up-arrow indicates that the limit is taken for values of x tending to xk from below, and the down-arrow indicates that the limit is taken for values of x tending to xk from above.
What we see from the examples is that where a function has a discontinuity, the Fourier series, when truncated to a large but finite number of terms, takes on a value between the right and left limits. The theorem says that the Fourier series finds the average of the two possibilities.
Theorem III.6. Suppose that f(x) and f'(x) are piecewise continuous on a finite interval [a,b]. Then the Fourier series (3.2) converges at every value of x between a and b as follows:
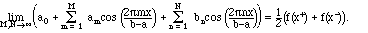
At the end points, we have:
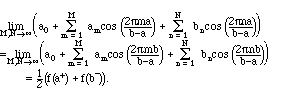
The limit at the end points is reasonable, because when the function is extended periodically, they are effectively the same point. And a particular consequence is that: At places where such a function is continuous, the Fourier series does indeed converge to the function.
In addition, if the function is continuous on the interval [a,b], and f(a) = f(b), then we can state a bit more, namely that the Fourier series converges uniformly to the function. This means that the error can be estimated independently of x:
Definition III.7.
A sequence of functions {fk(x)} converges uniformly on
the set 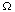 to a function g provided that
to a function g provided that
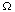 ) tending to 0.
(Follow
this link for some examples and
remarks about convergence of a sequence of functions.)
) tending to 0.
(Follow
this link for some examples and
remarks about convergence of a sequence of functions.)
The following theorem gives a general condition guaranteeing uniform convergence of Fourier series.
Theorem III.8. Suppose that f'(x) is piecewise continuous, f(x) itself is continuous on a finite interval [a,b], and f(a) = f(b). Then
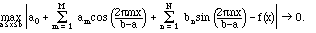
The condition that f(a) = f(b) is again reasonable if you think of f as a periodic function extending beyond the interval [a,b] - the extended function would be discontinuous at the end points if f(a) did not match f(b).
III.1. Find the entire
Fourier series (full sine and cosine series)
on the interval 0 <= x <= L for the function f(x) = x for 0 <= x <= L/2, otherwise 0. Discuss what happens if the series is evaluated outside the interval 0 <= x <= L.
III.2. Numerically find the first eight terms in the
Fourier series (full sine and cosine series)
on the interval 0 <= x <= 2 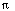 for the function f(x) = cosh(cos(x)).
for the function f(x) = cosh(cos(x)).
III.3. Find the (full) Fourier series of the following functions:
(i) cosh(2x), -
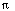 <= x <=
<= x <=
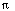
(ii) x|x|, -
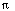 <= x <
<= x <
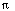 . Notice
that this is an odd
function.
. Notice
that this is an odd
function.
(iii) 1 - |x|, -1 <= x <= 1.
(iv) |sin(x)|, 0 <= x <=
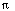 .
.
(v) 2 - 2 cos(
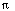 x), -1 <= x <= 1.
x), -1 <= x <= 1.
(vi) f(x) = x for 0 <= x < L/2, 0 for L/2 <= x < L
(Implicitly, the functions are extended periodically from these basic intervals.)
III.4. When the Fourier series for the square pulse and for x mod L are calculated in the next chapter, we find that am = 0 for all m >=1. Explain why, using ideas about symmetry.
III.5. a) Is it possible for a sequence of functions to converge in the r.m.s. sense for 0<=x<=1, to converge at every point of the interval 0<=x<=1/2, but not converge at any point of the interval 1/2<x<=1? Give an example or explain why not.
b) Is it possible for a sequence of square-integrable functions to converge at every point of the interval 0<=x<=1, but not converge in the r.m.s. sense? Give an example or explain why not.
III.6. Use the Parseval formula (3.4) to calculate
<3 + cos(x) + sin(x) + 2cos(2x) + 2sin(2x) + 3cos(3x), 1- sin(2x) - sin(4x)>
(standard inner product for 0<=x<=2
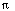 ), without doing any
integrals.
), without doing any
integrals.